Unidad 1: Derivadas de una funcion y tecnicas de derivacion
En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.
Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.
Tecnicas o reglas de derivación
Derivada de una función de grado n
Cabe hablar de la derivada de una función potencial de exponente real sin mencionar grado. Por ejemplo 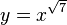 que es más fácil considerando
que es más fácil considerando 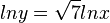
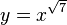 que es más fácil considerando
que es más fácil considerando 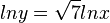
Algunos tipos de este tipo de funciones son: Función cuadrática, función cúbica, entre otras.
Pasos para cada tipo de derivación
1. Constantes- En este caso todas las derivadas de una constante son iguales a cero.
2. Función identidad- cualquier variable como a, b, c su derivada es 1. f(x)= entonces f'(x)=1
3. Regla de las potencias- Si se tiene un termino que esta elevado a una potencia en una función
 Formula:
Formula: 
4. Regla del factor constante- 1.Se deriva la x con la regla de las potencias. 2.Se multiplica el resultado por la constante (el número normal) Fórmula: f ‘(x)=(a)nxn-1

5. Regla de la suma- Se deriva con las reglas anteriores a cada termino de la función. Si F(x)=g(x)+f(x) entonces F’(x)=g ‘(x)+f ‘(x)
6. Regla de la diferencia- Se realizan los mismos pasos que en la regla de la suma igual pero restando.
7. Regla del producto- 1.Identificar las dos funciones, 2.Multiplicar la primera (u) por la derivada de la segunda (v), y se suma el producto de la segunda por la derivada de la primera. Formula: f ‘(x)=uv’+vu’
8. Regla de la derivada del cociente- 1.Identificar las dos funciones u y v, 2.Multiplicar la derivada de la primera (u) por la segunda (v), y se resta el producto de la primera por la derivada de la segunda, 3. Dividir todo entre la segunda al cuadrado. Formula: f ’(x)=vu’-v’u/v^2
Por ejemplo la función:
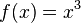
Lo primero es "bajar" el exponente de tal forma que éste multiplique a la variable con respecto a la cual estamos derivando, luego al mismo exponente se le resta la unidad formando uno nuevo, así:
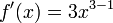
Quedando finalmente:

Considérese la función 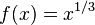
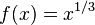
Se tiene:
Derivada de una constante por una función
Cuando una función esté representada por medio de  , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
Consideremos la siguiente función: 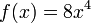 , lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:
, lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:
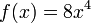 , lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:
, lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:
Para obtener
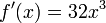
Cuando una constante acompaña a una variable cuyo exponente es 1 su derivada será el valor de la constante:

Entonces su derivada con respecto a esta variable será:
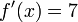
Puesto que 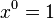
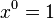
Derivada de una suma
Se puede demostrar a partir de la definición de derivada, que la derivada de la suma de dos funciones es la suma de las derivadas de cada una.
Es decir,  o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](https://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
 o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](https://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
Como ejemplo consideremos la función 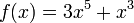 , para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
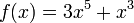 , para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función: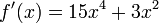
Téngase presente que la derivada, teniendo en cuenta que 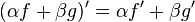 es una aplicación lineal en el conjunto de las funciones reales derivables. 2
es una aplicación lineal en el conjunto de las funciones reales derivables. 2
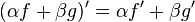 es una aplicación lineal en el conjunto de las funciones reales derivables. 2
es una aplicación lineal en el conjunto de las funciones reales derivables. 2Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función sin derivar."
Y matemáticamente expresado por la relación 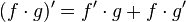 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:
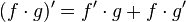 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo: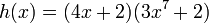
Identificamos a  y
y  , utilizando las reglas anteriormente expuestas, vemos que:
, utilizando las reglas anteriormente expuestas, vemos que:
 y
y  , utilizando las reglas anteriormente expuestas, vemos que:
, utilizando las reglas anteriormente expuestas, vemos que: y que
y que 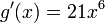
Por lo tanto
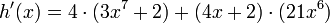
Simplificando y organizando el producto obtenido nos queda:
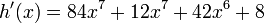
Sumamos términos semejantes y finalmente obtenemos la derivada:

Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir 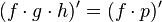 en donde
en donde  (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).
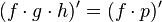 en donde
en donde  (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).Derivada de un cociente
La derivada de un cociente se determina por la siguiente relación:
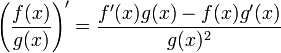
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:

Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es  y se multiplique por la derivada del numerador que seria
y se multiplique por la derivada del numerador que seria 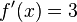 ; luego la segunda parte dice que tomemos la función del numerador (
; luego la segunda parte dice que tomemos la función del numerador ( ) sin derivar y lo multipliquemos por la derivada de
) sin derivar y lo multipliquemos por la derivada de  , que seria
, que seria 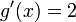 , todo esto lo dividimos entre el denominador al cuadrado, así:
, todo esto lo dividimos entre el denominador al cuadrado, así:
 y se multiplique por la derivada del numerador que seria
y se multiplique por la derivada del numerador que seria 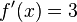 ; luego la segunda parte dice que tomemos la función del numerador (
; luego la segunda parte dice que tomemos la función del numerador ( ) sin derivar y lo multipliquemos por la derivada de
) sin derivar y lo multipliquemos por la derivada de  , que seria
, que seria 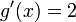 , todo esto lo dividimos entre el denominador al cuadrado, así:
, todo esto lo dividimos entre el denominador al cuadrado, así:
Ahora todo es cuestión de simplificar:
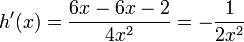
Regla de la cadena
La regla de la cadena es una fórmula para calcular la derivada de la composición de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la función compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)] es
o escrito en notación de Leibniz
Otras reglas
Funciones inversas y diferenciación
- Si
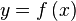 ,
, - entonces
 ,
, - y si
 y su inversa
y su inversa 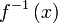 son diferenciables,
son diferenciables, - entonces
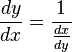 para los casos en que
para los casos en que  y cuando
y cuando  ,
,
Derivada de una variable con respecto a otra cuando ambas son funciones de una tercera variable
- Sea
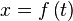 y
y  .
. - entonces
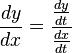
Diferenciación implícita
- Si
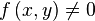 es una función implícita,
es una función implícita, - se tiene que:

Derivadas de funciones logarítmicas y exponenciales
Lo anterior es válido para todo c, pero para c < 0 el resultado es un número complejo.
Lo anterior es válido para todo c, pero para c < 0 el resultado es un número complejo.
Derivada de funciones trigonométricas
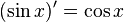 | 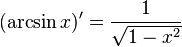 |
 | 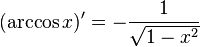 |
 |  |
 |  |
 |  |
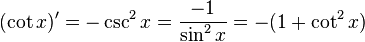 | 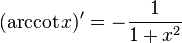 |
Derivada de funciones hiperbólicas
 |  |
 | 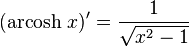 |
 | 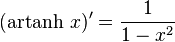 |
 |  |
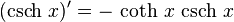 |  |
 | 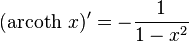 |
Unidad 2: Integral indefinida
En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir,F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 yF2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
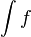 ó
ó 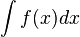
El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.
Ejemplo
Una primitiva de la función 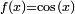 en
en  es la función
es la función  ya que:
ya que:
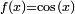 en
en 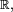 es la función
es la función  ya que:
ya que:
Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.
Constante de integración
La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque (F + C) ' = F ' + C ' = F ' + 0 = F '. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.
Para interpretar el significado de la constante de integración se puede observar el hecho de que la función f (x) es la derivada de otra función F (x), es decir, que para cada valor de x, f (x) le asigna la pendiente de F (x). Si se dibuja en cada punto (x, y) del plano cartesiano un pequeño segmento con pendiente f (x), se obtiene un campo vectorial como el que se representa en la figura de la derecha. Entonces el problema de encontrar una función F (x) tal que su derivada sea la función f (x) se convierte en el problema de encontrar una función de la gráfica de la cual, en todos los puntos sea tangente a los vectores del campo. En la figura de la derecha se observa como al variar la constante de integración se obtienen diversas funciones que cumplen esta condición y son traslaciones verticales unas de otras.
Otras propiedades
Linealidad de la integral indefinida
La primitiva es lineal, es decir:
- Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.
- Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.
La linealidad se puede expresar como sigue:
La primitiva de una función impar es siempre par
En efecto, como se ve en la figura siguiente, las áreas antes y después de cero son opuestas, lo que implica que la integral entre -a y a es nula, lo que se escribe así: F(a) - F(-a) = 0, F siendo una primitiva de f, impar. Por lo tanto siempre tenemos F(-a) = F(a): F es par.
La primitiva F de una función f par es impar con tal de imponerse F(0) = 0
En efecto, según la figura, las áreas antes y después de cero son iguales, lo que se escribe con la siguiente igualdad de integrales:
Es decir F(0) - F(-a) = F(a) - F(0). Si F(0) = 0, F(-a) = - F(a): F es impar.
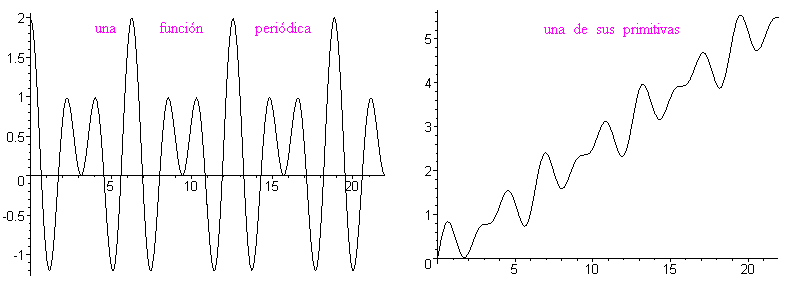
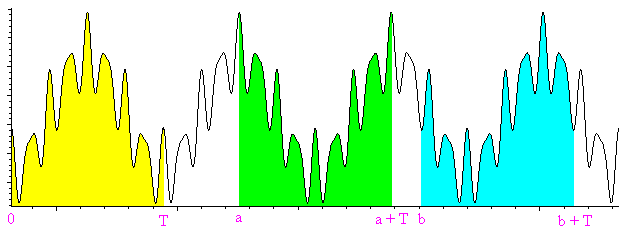
La primitiva de una función periódica es la suma de una función lineal y de una función periódica
Para probarlo, hay que constatar que el área bajo una curva de una función periódica, entre las abcisas x y x + T (T es el período) es constante es decir no depende de x. La figura siguiente muestra tres áreas iguales. Se puede mostrar utilizando la periodicidad y la relación de Chasles, o sencillamente ¡con unas tijeras! (cortando y superponiendo las áreas de color).
En término de primitiva, significa que F(x + T) - F(x) es una constante, que se puede llamar A. Entonces la función G(x) = F(x) - Ax/T es periódica de período T. En efecto G(x + T) = F(x + T) - A(x + T)/T = F(x) + A - Ax/T - AT/T = F(x) - Ax/T = G(x). Por consiguiente F(x) = G(x) + Ax/T es la suma de G, periódica, y de Ax/T, lineal.
Relación entre la integral de una función y la de su recíproca
Para simplificar, se impone f(0) = 0; a es un número cualquiera del dominio de f. Entonces tenemos la relación:
El área morada es la integral de f, el área amarilla es la de f -1, y la suma es el rectángulo cuyos costados miden a y f(a) (valores algebraicos). Se pasa de la primera curva, la de f, a la segunda, la de f -1 aplicando la simetría axial alrededor de la diagonal y = x.
El interés de esta fórmula es permitir el cálculo de la integral de f -1 sin conocer una primitiva; de hecho, ni hace falta conocer la expresión de la recíproca.
Existencia de primitivas
Cualquier función continua sobre  admite localmente una antiderivada o primitiva. Sin embargo en espacios de dimensión finita la continuidad no garantiza la existencia de antiderivadas. Una condición suficiente de existencia de antiderivadas es que la imagen pertenezca a un espacio vectorial conveniente, también llamado
admite localmente una antiderivada o primitiva. Sin embargo en espacios de dimensión finita la continuidad no garantiza la existencia de antiderivadas. Una condición suficiente de existencia de antiderivadas es que la imagen pertenezca a un espacio vectorial conveniente, también llamado  -completo. La propiedad definitoria de dichos espacios es que toda función
-completo. La propiedad definitoria de dichos espacios es que toda función 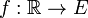 con
con 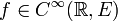 admite una función primitiva. Si el espacio no es
admite una función primitiva. Si el espacio no es  -completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.
-completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.
 admite localmente una antiderivada o primitiva. Sin embargo en espacios de dimensión finita la continuidad no garantiza la existencia de antiderivadas. Una condición suficiente de existencia de antiderivadas es que la imagen pertenezca a un espacio vectorial conveniente, también llamado
admite localmente una antiderivada o primitiva. Sin embargo en espacios de dimensión finita la continuidad no garantiza la existencia de antiderivadas. Una condición suficiente de existencia de antiderivadas es que la imagen pertenezca a un espacio vectorial conveniente, también llamado  -completo. La propiedad definitoria de dichos espacios es que toda función
-completo. La propiedad definitoria de dichos espacios es que toda función 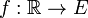 con
con 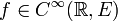 admite una función primitiva. Si el espacio no es
admite una función primitiva. Si el espacio no es  -completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.
-completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.Cálculo de primitivas
Integrales inmediatas
Para encontrar una primitiva de una función dada, basta con descomponerla (escribirla bajo forma de una combinación lineal) en funciones elementales cuyas primitivas son conocidas o se pueden obtener leyendo al revés una tabla de derivadas, y luego aplicar la linealidad de la integral:
Aquí están las principales funciones primitivas:
Función  : primitiva de : primitiva de 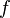 | función 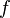 : derivada de : derivada de  |
|---|---|
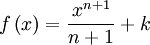 |  |
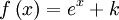 | 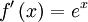 |
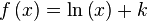 |  |
 |  |
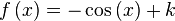 |  |
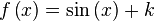 |  |
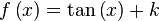 |  |
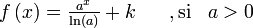 | 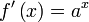 |
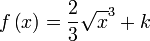 |  |
 |  |
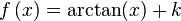 |  |
Por ejemplo, busquemos una primitiva de x → x(2-3x). Como no se conocen primitivas de un producto, desarrollemos la expresión: x(2-3x)= 2x - 3x2. 2x es la derivada de x2, 3x2 es la de x3, por lo tanto 2x - 3x2 tiene como primitiva x2 - x3 + k. Si además se pide que la primitiva verifique una condición F(x0) = y0 (que recibe el nombre de condición inicial cuando se trata de un problema de física), entonces la constante k es unívocamente determinada. En el ejemplo, si se impone F(2) = 3, entonces forzosamente k = 7.
Métodos de integración
Tenemos varios métodos a nuestra disposición:
- La linealidad de la integración nos permite descomponer integrales complicadas en otras más sencillas.
- Integración por sustitución, a menudo combinada con identidades trigonométricas o el logaritmo neperiano.
- Integración por partes para integrar productos de funciones.
- El método de la regla de la cadena inversa, un caso especial de la integración por sustitución.
- El método de fracciones parciales nos permite integrar todas las funciones racionales (fracciones de dos polinomios).
- El algoritmo de Risch.
- Integrales también pueden calcularse utilizando tablas de integrales.
Unidad 3: Metodos de Integracion
Se entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.
Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que
,
lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada:
.
Generalidades
El problema de resolver una integral indefinida o buscar una primitiva es mucho más complicado que el problema de calcular la derivada de una función. De hecho, no existe un algoritmo determinista que permita expresar la primitiva de una función elemental, es más, la primitiva de muchas funciones elementales de hecho no es ninguna función elemental. Por ejemplo, no existe ninguna función elemental F(x) que sea tal que:
Si se consideran grupos de funciones elementales de un cierto tipo (polinómicas, fracciones racionales, trigonométricas, etc.) entonces el problema de encontrar la primitiva puede resolverse con problemas elementales llamados métodos de integración como los tratados a continuación.
Integración directa
En ocasiones es posible aplicar la relación dada por el teorema fundamental del cálculo de forma directa. Esto es, si se conoce de antemano una función cuya derivada sea igual a f(x) (ya sea por disponer de una tabla de integrales o por haberse calculado previamente), entonces tal función es el resultado de la antiderivada. La integración directa requiere confeccionar una tabla de funciones y sus antiderivadas o funciones primitivas.
- Ejemplo
- Calcular la integral indefinida
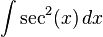 .
. - En una tabla de derivadas se puede comprobar que la derivada de
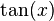 es
es 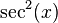 . Por tanto:
. Por tanto: 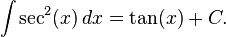
- Ejemplo
- Calcular la integral indefinida
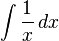 .
. - Una fórmula estándar sobre derivadas establece que
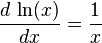 para x>0. De este modo, se podría responder que la solución al problema es
para x>0. De este modo, se podría responder que la solución al problema es  , pero hay que tener en cuenta que la fórmula sólo es válida para valores positivos de x. La restricción es muy razonable, ya que la función
, pero hay que tener en cuenta que la fórmula sólo es válida para valores positivos de x. La restricción es muy razonable, ya que la función  no está definida para valores reales negativos o 0. Sin embargo, para valores negativos también existe una integral indefinida de
no está definida para valores reales negativos o 0. Sin embargo, para valores negativos también existe una integral indefinida de  , que es
, que es  . Para incluir ambos casos, se dice que la solución es
. Para incluir ambos casos, se dice que la solución es 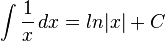 .
.
Este último ejemplo muestra que es muy importante saber en qué intervalo son válidas las fórmulas encontradas en las tablas de integrales.
Funciones analíticas
El problema de integración es trivial si se consideran funciones analíticas y se admite como primitivas potencias de series formales ya que:
Método de integración por sustitución
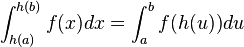
El método de integración por sustitución o por cambio de variable se basa en realizar un reemplazo de variables adecuado que permita convertir el integrando en algo sencillo con una integral o antiderivada simple. En muchos casos, donde las integrales no son triviales, se puede llevar a una integral de tablapara encontrar fácilmente su primitiva. Este método realiza lo opuesto a la regla de la cadena en la derivación.
Ejemplo #1
Suponiendo que la integral a resolver es:
En la integral se reemplaza  con
con 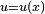 :
:
 con
con 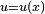 :
:(1)
Ahora se necesita sustituir también 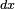 para que la integral quede sólo en función de
para que la integral quede sólo en función de  :
:
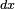 para que la integral quede sólo en función de
para que la integral quede sólo en función de  :
:
Se tiene que  por tanto derivando se obtiene
por tanto derivando se obtiene 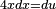 . A continuación se despeja
. A continuación se despeja 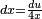 y se agrega donde corresponde en ():
y se agrega donde corresponde en ():
 por tanto derivando se obtiene
por tanto derivando se obtiene 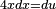 . A continuación se despeja
. A continuación se despeja 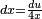 y se agrega donde corresponde en ():
y se agrega donde corresponde en ():
Simplificando:
Hay que considerar si la sustitución fue útil y por tanto se llegó a una forma mejor, o por el contrario empeoró las cosas. Luego de adquirir práctica en esta operación, se puede realizar mentalmente. En este caso quedó de una manera más sencilla dado que la primitiva del coseno es el seno.
Como último paso antes de aplicar la regla de Barrow con la primitiva, hay que modificar los límites de integración. Sustituyendo x por el límite de integración, se obtiene uno nuevo. En este caso, como se hizo  :
:
 :
:
(límite inferior)
(límite superior)
Tras realizar esta operación con ambos límites la integral queda de una forma final:
Ejemplo #2
Suponiendo ahora que la integral a resolver es:
Cuando las integrales son de tipo racional e involucra funciones trigonométricas, dígase: 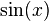 y
y  la sustitución conveniente resulta ser
la sustitución conveniente resulta ser 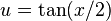 :
:
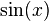 y
y  la sustitución conveniente resulta ser
la sustitución conveniente resulta ser 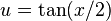 :
: ,
, 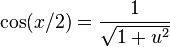
Entonces (por Teorema de la suma y la resta)

por otra parte 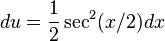 o
o 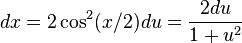
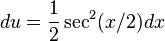 o
o 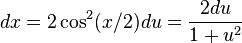
la integral queda después de dicha sustitución:
Método de integración por partes
El método de integración por partes es el que resulta de aplicar el siguiente teorema:
.
Desde un punto de vista didáctico se recomienda escoger la función u de acuerdo con el orden:[cita requerida]
- Trigonométrica Inversa
- Logarítmica
- Algebraica o polinómica
- Trigonométrica
- Exponencial.
Otra recomendación sería cambiar el orden de trigonométrica y exponencial. Si seguimos esta otra recomendación podemos usar la regla mnemotécnia ALPES, asignándole el puesto de u de acuerdo con el orden de aparición:
- Arcoseno(y cualquier trigonométrica inversa)
- Logarítmica
- Polinómica
- Exponencial
- Seno/coseno(y cualquier trigonométrica)
Para deducir la fórmula se puede partir de la derivada del producto de dos funciones: 

Multiplicando por 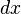 se obtiene
se obtiene  . Integrando ambos miembros en la ecuación se tiene.
. Integrando ambos miembros en la ecuación se tiene. 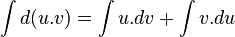
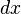 se obtiene
se obtiene  . Integrando ambos miembros en la ecuación se tiene.
. Integrando ambos miembros en la ecuación se tiene. 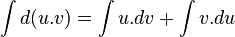
Como la integral y el diferencial son operaciones inversas se tiene. 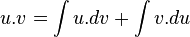 ; despejando:
; despejando: 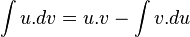
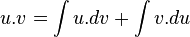 ; despejando:
; despejando: 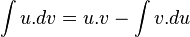
Método de integración por cambio de variables
El cambio de variables es uno de los métodos más usados en la integración. Permite expresar la integral inicial mediante un nuevo integrando y un nuevo dominio siendo la integral equivalente a la primera. Para integrales simples de una sola variable si  es la variable original y
es la variable original y 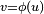 es una función invertible, se tiene:
es una función invertible, se tiene:
 es la variable original y
es la variable original y 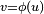 es una función invertible, se tiene:
es una función invertible, se tiene:Integrales de funciones trigonométricas
Con carácter general un cambio que resulta muchas veces útil expresar las potencias funciones trigonométricas mediante funciones de ángulos múltiples, eso puede lograrse gracias a las siguientes identidades:
Por ejemplo las dos fórmulas anteriores permiten substituir potencias complejas de la función coseno por el coseno de ángulos múltiplo:
Integral que contiene potencias de senos y cosenos 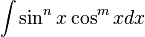
- En general, se intenta escribir un integrando en el que intervienen potencias de seno y coseno en una forma donde se tiene sólo un factor seno (y el resto de la expresión en términos de coseno) o sólo un factor coseno (y el resto de la expresión en términos de seno).
- La identidad
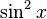

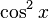

 permite convertir de una parte a otra entre potencias pares de seno y coseno.
permite convertir de una parte a otra entre potencias pares de seno y coseno.
- Existen 3 casos:
Cuando n es impar
Cuando 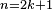 , podemos apartar un factor del seno y sustituirlo por la identidad
, podemos apartar un factor del seno y sustituirlo por la identidad 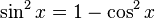 para poder expresar los factores restantes en términos del coseno:
para poder expresar los factores restantes en términos del coseno:
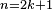 , podemos apartar un factor del seno y sustituirlo por la identidad
, podemos apartar un factor del seno y sustituirlo por la identidad 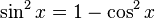 para poder expresar los factores restantes en términos del coseno:
para poder expresar los factores restantes en términos del coseno:
Al tener el integral de esta forma se puede resolver por medio de sustitución haciendo  ,
,  . Como en la expresión no tenemos un
. Como en la expresión no tenemos un 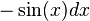 multiplicamos ambos lados por
multiplicamos ambos lados por 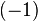 y nos queda la expresión
y nos queda la expresión 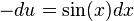 que ya podemos sustituir:
que ya podemos sustituir:
 ,
,  . Como en la expresión no tenemos un
. Como en la expresión no tenemos un 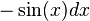 multiplicamos ambos lados por
multiplicamos ambos lados por 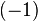 y nos queda la expresión
y nos queda la expresión 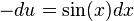 que ya podemos sustituir:
que ya podemos sustituir:Cuando m es impar
Cuando  , podemos de la misma manera apartar un factor de coseno y emplear
, podemos de la misma manera apartar un factor de coseno y emplear 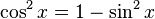 para poder expresar los factores restantes en términos del
para poder expresar los factores restantes en términos del  :
:
 , podemos de la misma manera apartar un factor de coseno y emplear
, podemos de la misma manera apartar un factor de coseno y emplear 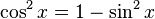 para poder expresar los factores restantes en términos del
para poder expresar los factores restantes en términos del  :
:
al hacer 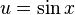 y
y  tendríamos
tendríamos
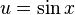 y
y  tendríamos
tendríamosCuando m y n son pares
Cuando dichas potencias son pares a la vez  y
y  , podemos aplicar las identidades de la mitad de ángulo:
, podemos aplicar las identidades de la mitad de ángulo:
 y
y  , podemos aplicar las identidades de la mitad de ángulo:
, podemos aplicar las identidades de la mitad de ángulo:
algunas veces es útil usar la identidad:
sería igual a:
Ejemplo #1
- Solución Lo primero que tenemos que ver es que la potencia impar la tiene la función seno, esto nos hace notar que estamos en el primer caso que describimos arriba, entonces aplicamos el algoritmo,
Sustituyendo  , tenemos
, tenemos  luego:
luego:
 , tenemos
, tenemos  luego:
luego:
Integrales que contiene potencias de tangentes y secantes 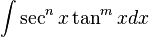
- Se puede usar una estrategia similar a la anterior.
- Puesto que:
-
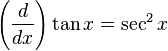 , se puede separar un factor
, se puede separar un factor 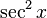 y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad
y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad  .
.
-
- O bien, puesto que:
-
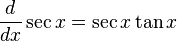 , se puede separar un factor
, se puede separar un factor 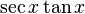 y convertir la potencia restante (par) de tangente a secante.
y convertir la potencia restante (par) de tangente a secante.
-
- Existen 3 casos:
Cuando n es par
 separar un factor de
separar un factor de  y utilice
y utilice 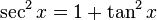 para lograr expresar los factores restantes en términos de
para lograr expresar los factores restantes en términos de 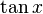 :
:
de esta manera podemos hacer  y
y 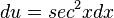 y el integral quedaría así:
y el integral quedaría así:
 y
y 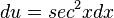 y el integral quedaría así:
y el integral quedaría así:Cuando m es impar
 apartar un factor de
apartar un factor de 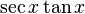 y emplear
y emplear 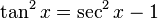 para poder expresar los factores que restan en términos de
para poder expresar los factores que restan en términos de  :
:
de esta manera se puede hacer 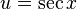 y
y  , con lo que queda
, con lo que queda
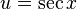 y
y  , con lo que queda
, con lo que queda
La tangente tiene potencia par 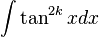
La Secante tiene potencia impar
En este caso se procede a integrar por partes.
Ninguno de los anteriores
Al no encontrar la forma de ninguno de los pasos anteriores, se traslada a 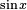 y
y 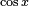 , recordando que:
, recordando que:
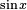 y
y 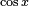 , recordando que:
, recordando que:
Para otros casos, las directrices no son tan claras. Podría ser necesario usar identidades, integración por partes y, ocasionalmente, un poco de inventiva.
- A veces será necesario poder integrar
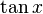 por medio de la fórmula establecida:
por medio de la fórmula establecida:
- Se necesitará también la integral indefinida de la secante:
- A veces será necesario poder integrar
Esta última se podría comprobar mediante la derivación de lado derecho, o como sigue:
- Primero se mutiplican numerador y denominador por
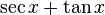 :
:
- Si se sustituye
 , después
, después  , también, la integral se convierte en:
, también, la integral se convierte en:
- Así, se tiene:
- NOTA: Para integrales que contienen cosecantes y cotangentes, la estrategia es análoga a la del par secantes-tangentes. Recordar la identidad:

Reducción a funciones racionales
Si el integrando puede expresar como una función racional de funciones trigonométicas:
(*)
Entonces el cambio:
permite reescribir la integral () como:
Que resulta ser una función racional, y por tanto, de integración mecánica.
Integrales de funciones racionales
Dada una función racional expresable como el cociente de dos polinomios:
Si el denominador es un polinómico mónico 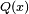 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
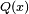 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
Si 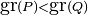 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
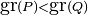 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
Por lo que la integral de la función  es una combinación lineal de funciones de la forma:
es una combinación lineal de funciones de la forma:
 es una combinación lineal de funciones de la forma:
es una combinación lineal de funciones de la forma:
Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la integración.
Integración numérica
La integración numérica comprende una amplia gama de algoritmos para calcular el valor numérico de una integral definida. A efectos prácticos se usa cuando no se conoce un método analítico de integración o la función primitiva resulta tan complicada que para una aplicación práctica resulta más útil buscar directamente su valor numérico. El término cuadratura numérica (a menudo abreviado a cuadratura) es más o menos sinónimo de integración numérica, especialmente si se aplica a integrales de una dimensión a pesar de que para el caso de dos o más dimensiones (integral múltiple) también se utiliza.
Unidad 4: integral definida
Desde su origen, la noción de integral ha respondido a la necesidad de mejorar los métodos de medición de áreas subtendidas bajo líneas y superficies curvas. La técnica de integración se desarrolló sobre todo a partir del siglo XVII, paralelamente a los avances que tuvieron lugar en las teorías sobre derivadas y en el cálculo diferencial.
Concepto de integral definida
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
La integral definida de la función entre los extremos del intervalo [a, b] se denota como:
Propiedades de la integral definida
La integral definida cumple las siguientes propiedades:
- Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
- Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
- La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
- La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
- Al permutar los límites de una integral, ésta cambia de signo.
- Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
- Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:
Ilustración gráfica del concepto de integral definida.
Función integral
Considerando una función f continua en [a, b] y un valor x Î [a, b], es posible definir una función matemática de la forma:
donde, para no inducir a confusión, se ha modificado la notación de la variable independiente de x a t. Esta función, simbolizada habitualmente por F (x), recibe el nombre de función integral o, también, función área pues cuando f es mayor o igual que cero en [a, b], F (x) nos da el área.
Interpretación geométrica de la función integral o función área.
Teorema fundamental del cálculo integral
La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:
A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:
- Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
- Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
- El valor de la integral definida entre estos dos puntos vendrá entonces dado por:
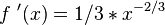
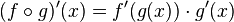
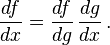
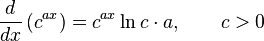
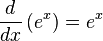



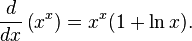
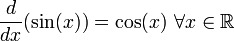




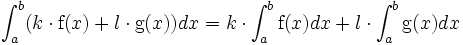
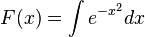
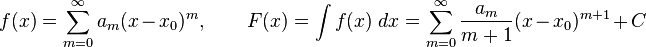
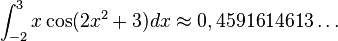


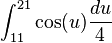
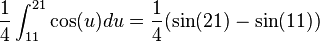




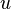 y
y  , puede simplificarse mucho la resolución de la
, puede simplificarse mucho la resolución de la 
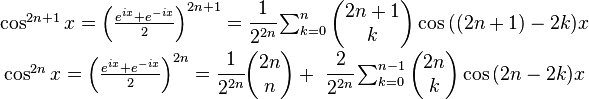

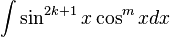




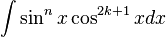


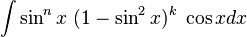

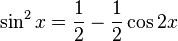
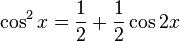
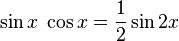
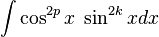
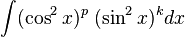
![\int [\frac{1}{2} + \frac{1}{2}\cos 2x]^{p}\;
[\frac{1}{2} - \frac{1}{2}\cos 2x]^{k} dx](https://upload.wikimedia.org/math/f/8/a/f8ad147bc91a1a82fa5309934f92f7e2.png)
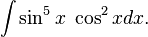


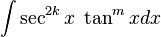
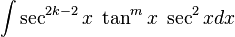
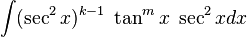
![\int [1 + \tan^{2}x]^{k-1}\;\tan^{m}x\;\sec^{2}xdx](https://upload.wikimedia.org/math/0/c/d/0cd003af7e7d615137156117e129d5e9.png)
![\int [1 + u^{2}]^{k -1}\;u^mdu](https://upload.wikimedia.org/math/e/3/e/e3e2074f101e0aecf783fb20fc3fc5a4.png)




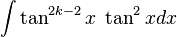

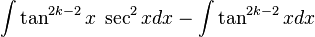


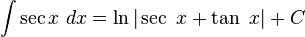
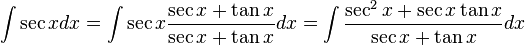


![\int R(\sin(x),\cos(x))\ dx, \qquad R(x,y)=\frac{P(x,y)}{Q(x,y)},\ P,Q\in \R[x,y]](https://upload.wikimedia.org/math/e/d/6/ed6d5e1e01fdce9440f3cb04afe21163.png)
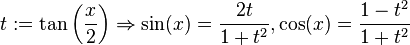
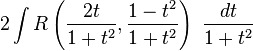
![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](https://upload.wikimedia.org/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)


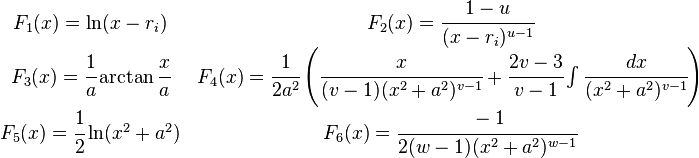
No hay comentarios:
Publicar un comentario